之前,我已经建立了一些基本的Python代码架构,并实现了最后进近航段的保护区主区和副区梯形轮廓的坐标串和绘图输出。final_protect_area(x_faf, final_leg)函数可以通过输入FAF点(“最后进近定位点”,即最后航段的起点)坐标和最后航段结构体(通过原生的namedtuple实现)来返回以多边形几何表示的最后段主区和副区。航段结构体包含提供引导的电台、航段长度及单位、航迹方向角,电台结构体又包含了点几何和类型。那么仿照这个例子,本次的起始进近保护区函数应该接受的输入则是该航段起止点(起始进近定位点IAF、中间进近定位点IF)的坐标和起始航段的信息,而返回的结果则同样是主副区的多边形几何。
以上接口定义方面看起来没有问题,接下来转入实现。要想仿照最后进近的编程模式,就要先回顾其实现的思路。最后航段必须有一个导航台提供引导,其保护区形状是一个等腰梯形。这个梯形可以理解为航径线的一个宽度(半径)不断变小的缓冲区,因此其几何由上底、下底、高来确定,而在航空交通中,很多梯形的形状是通过一条底边的长和腰与高的夹角(“扩张角”,或者其正切值,即宽度变化率,“扩张率”)给出。因此,这个图形的生成主要就是根据导航台的类型和位置、来确定这个梯形的底边长和宽度变化率。在此基础上,根据起点位置和航段长度截取出梯形在航段范围内的部分。
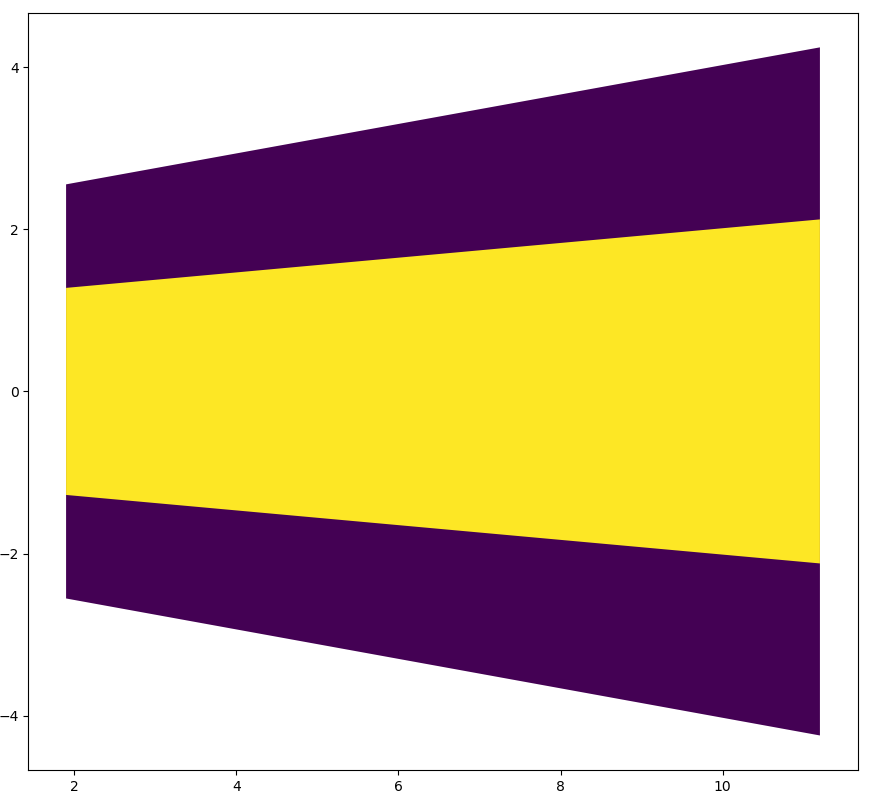
由于飞行程序设计通常在以跑道入口中点为原点的平面直角坐标系中进行,而本次最后段的航迹就是该坐标系X轴的负方向,所以梯形顶点Y坐标实际上就是梯形在起止点处两腰之间宽度的一半。由此思路,之前的实现编写了一个计算梯形宽度的函数生成器width_gen(facility, phase, unit=’km’),通过输入的导航台位置和类型信息,查询相应导航台的性能参数(即梯形底边长和扩张角),返回一个可以根据到导航台纵向(飞行方向)距离计算宽度的函数。这个思路由于将太多因素耦合在一起,对起始航段相对复杂情形的实现带来了很多阻碍,最终放弃了延续这个思路进行开发。
起始航段的尝试与思考
正常情况下,起始航段是一个半径为5海里的缓冲区,即一个以预定路线为中心的矩形。但是导航台的位置和航段的长度可能引入缩减和扩张两类不互斥的特殊情况。缩减的情况是,如果起始段终点(IF)处设置了一个导航台,则此处的缓冲半径(宽度)相应减小,再逆飞行方向线性扩张到正常宽度。扩张的情况是,如果起始段起点(IAF)距提供引导的导航台太远,则超过一定距离后要从正常宽度的基础上按参数扩张。
模仿思路的误区
在实现中,模仿最后段半宽计算思路面临一个巨大的不确定因素,即提供引导的导航台是否在IF处。这一点似乎牵涉到扩张情形的距离判定:如果在,则到电台的距离和航段中的相对位置是相等的;如果不在,到电台的距离与在航段中的相对位置是不同的。受最后航段等腰梯形到底边距离与宽度关系这个思路的影响,此处很容易陷入混乱。要做到一个同样的保护区宽度函数生成器,这个生成的函数的参数就要在距底边(电台)长度和距航段终止点(或者跑道入口)长度之间作出明确和转换,而这又取决于导航台与航段的相对位置。而这时,只能回到原点重新设计这个函数。
实现初期还因为理论知识不熟悉遇到一个相关误区,即试图考虑两个导航台的情况。诚然,最后航段必须有一个导航台,但如果IF是导航台,起始航段则只会跟它有关。虽然这时确实有两个导航台存在,但在起始航段保护区绘制中仍然不需要考虑两个导航台的情形,缩减和扩张都以IF处的台为基础。
工程规范的梳理
首先,两种特殊情况是可能同时存在的,这就至少有四种可能:正常(既没有缩减、也没有扩张)、只有缩减、只有扩张、既有缩减也有扩张。但是,只有缩减的情况还可以细分,因为按规定参数扩张到正常宽度是需要一定距离的,实际上航段的长度并非一定足够完成这个动作。因此,只有缩减又分为了只有缩减且长度足够恢复正常、只有缩减但长度不足以恢复正常。这五种情况对应的几何形状是不同的,正常情况为矩形,缩减够长是矩形和IF附近梯形的拼接,缩减过短是只有一个梯形,只有扩张是IAF附近梯形和矩形的拼接,都有是IAF附近梯形、矩形、IF附近梯形三者的拼接。
起始段实现思路与过程
抛弃了半宽计算的思路,保护区生成本质上是确定多边形区域顶点坐标。起始段的多边形相较于最后段,其难点在于多边形结构不确定,进而顶点数量和位置不确定。当然,分别为五种情况实现一个判定函数和一个顶点坐标计算函数肯定是可行的,只是冗余太多,容易在调试修改中造成逻辑不一致或者重复计算等情况。而要写成一个流程,潜在的难点有两处:在什么地方按什么条件设置分支;如何处理变长坐标串。
分支判定与流程设计
根据上文的梳理,可以按有无缩减、有无扩张分为四种,再按缩减是否恢复再将第二种分为两种。有无缩减可以通过比较导航台位置和IF位置判定,有无扩张则可以通过计算导航台位置和IAF位置之间的距离、再与规定的阈值比较判定。缩减是否恢复可以通过比较航段长度(或IAF和IF间距)和规定的阈值判定。
变长的顶点坐标串则可以通过向一个列表中依次加入元素实现。而且,由于图形的对称性,只需要加入一侧的点,再逆序加入其相反数即可。所以,最好能按合理的顺序进行上述判定,以便在完成判定后能够按正确的顺序追加顶点。从IF点处开始,逆进近方向,保护区外轮廓第一个顶点的X坐标是IF的X坐标,Y坐标则依赖于是否缩减。如果缩减,第二个可能的顶点是缩减后恢复正常的点,如果缩减距离过近强制恢复,这个点则是这半边的最后一点(需结束后续判定);如果是缩减后完成恢复,则其X坐标需要计算(也可以是规定的阈值,考虑到规定值舍入误差的存在,此处取计算所得的精确点)。第三个可能的顶点是正常宽度的终点,其Y坐标为规定的标准值,X坐标取决于是否扩张,若无扩张,即为IAF的X坐标(完成判定);若有扩张,则需要计算(同上,不考虑舍入误差可直接采用规定的阈值)。同样,在扩张的情况下,还存在第四个可能的顶点,即扩张的IAF,其Y坐标需要计算。
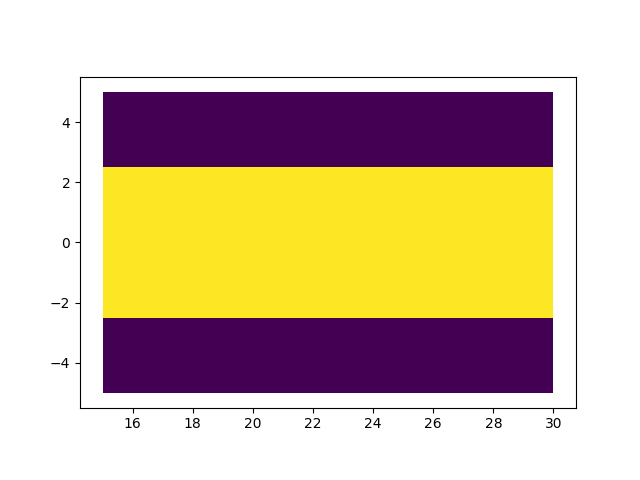
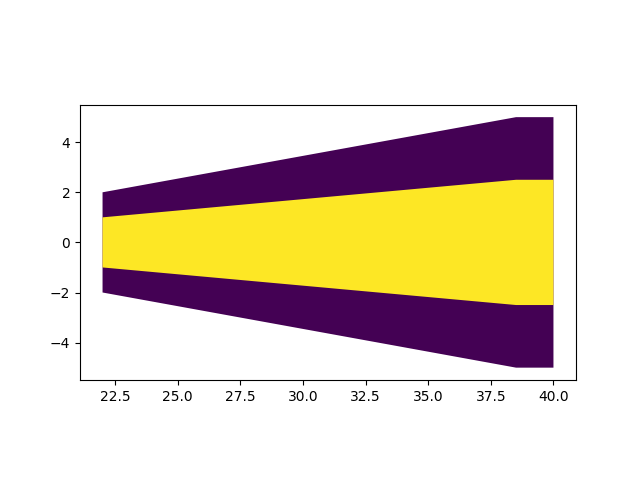
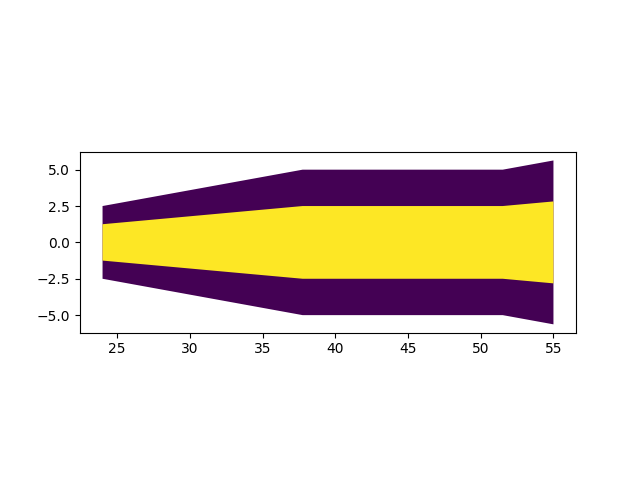
后处理与测试收尾
构建好的顶点坐标串,生成多边形几何只需用到原生的集合操作工具map(映射,用于取相反数)、reverse(逆序),以及基本的列表操作。最后不要忘记的一点是,重复首点以完成闭合。由于这个功能较为常用,同时也适用于中点连中点作主副区分界线的场景,因此将其封装为make_buf_geom_from_hw(locs, hwidths, primary)函数供重复调用。
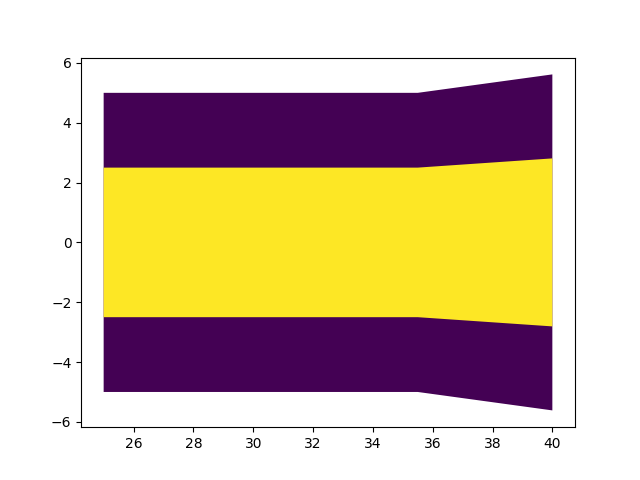
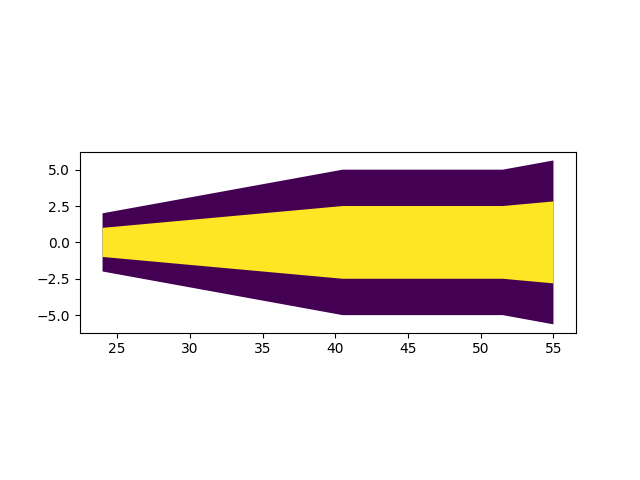
测试也不能少。有了上述五类情形的分析,自然就可以设计每种情形的测试用例。在编写和运行测试的过程中,还发现了两处小问题,其中一个可以直接解决、另一个有待后续完善。直接解决的是,发现既有缩减又有扩张的情况下,扩张开始位置与规定阈值相关过大、非常明显。如图,设置的NDB电台位于跑道入口外24海里,按ICAO Doc 8168 Vol 2 Part I Section 4 Chapter 3 Appendix B 第4页图I-4-3-App B-4-3 IAF距NDB超过25.5公里(13.8海里)的情况,NDB缩减恢复正常的距离是13.8海里,因而测试用例中的位置应该是跑道入口外37.8海里,但图示结果明显超过了40海里。经检查,原来是配置文件中输入的起始宽及扩张角规定值将两种电台搞反了,纠正后即可恢复正常。
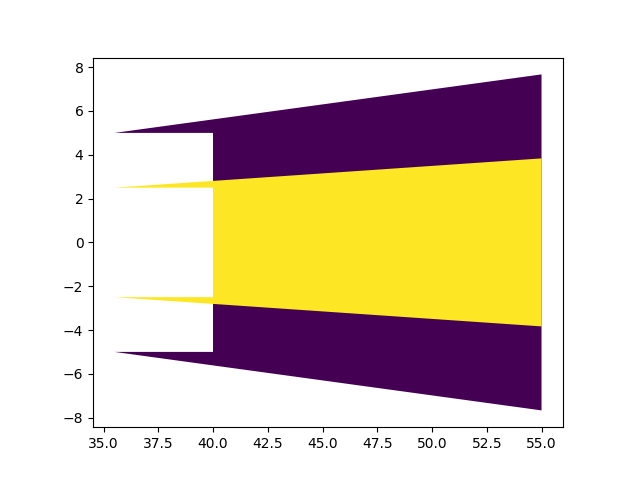
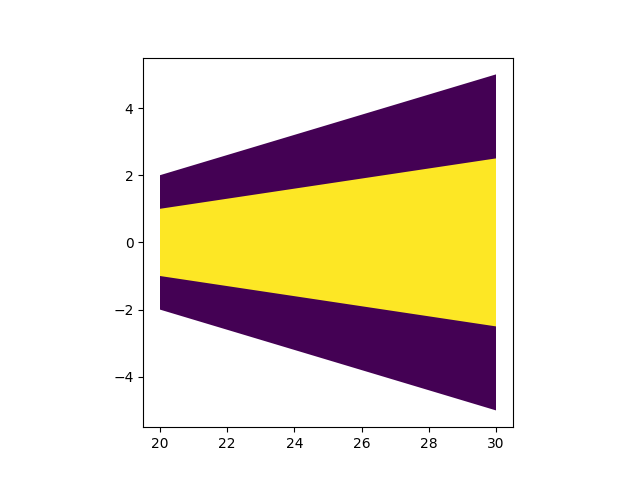
测试中发现的另一个问题是,如果IF距离跑道入口过远且无导航台,仅扩张的情况下梯形与矩形的拼接体出现异常形状。如图测试值为VOR台设在入口内1海里,IF设在入口前40海里,此时中间加最后航段的长度显然超过了规定的最大值15+10=25海里,而本次编写的程序未验证这一基本设计规则。当然,这个验证也不该是绘制保护区时要考虑的事情,因此留待以后处理。